Главная

Компьютерные тренажеры · Обзорная статья · Конструктор · Тренажеры (продукты) · Теплосети · Как заказать

SCADA

Другие проекты · Сад Слов · Almik

Публикации · Основные публикации · Блог ЖЖ · Путешествия · Живопись . Лирика

Об авторе

Донской А.Н.
г.Чебоксары, кафедра САУЭП ЧувГУ
1999

Моделирование является важной составной частью исследования и проектирования технических систем различного назначения (в частности, систем автоматического управления - САУ). Наиболее удобным способом моделирования является использование специальных программных средств (далее ПС), позволяющих легко составлять модели в виде структурных (функциональных) схем из набора стандартных элементов. Такой подход позволяет легко осуществить имитационное моделирование и провести исследования динамики с учетом всех существенных особенностей исследуемой системы (нелинейности, динамически изменяемые параметры, внешние воздействия).

Наиболее распространенным и простым видом анализа является анализ динамики - получение переходных процессов в системе под действием тех или иных внешних воздействий, по результатам которого можно оценить такие показатели качества, как перерегулирование и время регулирования. Однако часто требуются более сложные исследования, например, зависимости показателей качества от тех или иных параметров системы. Задача синтеза предполагает оптимизацию ряда параметров системы по заданным критериям качества. В данной статье описываются возможности проведения сложных исследований переходных процессов при помощи ПС АЛМИК.

1. Подходы к автоматизации сложных исследований.

Ввиду отсутствия аналитического решения для произвольных нелинейных динамических систем метод имитационного моделирования обусловливает единственный вариант исследования - многовариантный анализ [3]. При этом ПС обеспечивает изменение параметров модели и для каждого набора параметров повторяет расчет переходного процесса в модели. Результаты моделирования (далее - "показатели") сохраняются и могут быть представлены в виде зависимостей от значений параметров.

В задаче параметрической оптимизации варьирование параметров производится с применением каких-либо градиентных методов с целью оптимизации показателей.

Наконец, задача синтеза обычно предполагает автоматическую генерацию и настройку параметров корректирующего устройства исходя из заданных критериев качества.

Особой разновидностью анализа является частотный анализ, результаты которого (амплитудно-частотные характеристики) могут использоваться для оценки качества и устойчивости системы. Здесь могут быть использованы три пути:

• численно-аналитический расчет (для линейных систем);
• численно-аналитический расчет или имитационное моделирование (в частотной области) с применением метода гармонической линеаризации (может быть применен также к модели, описанной в виде структурной схемы при соответствующей поддержке ПС);
• имитационное моделирование (во временной области) при подаче на вход модели гармонического сигнала с непрерывно изменяемой (скользящей) частотой и измерении амплитуды и фазы сигнала на выходе модели.

Последний способ является наиболее медленным из-за большого объема численных расчетов, но легче всего поддается автоматизации и хорошо отражает реальное поведение исследуемой системы при условии достаточно малого шага интегрирования и достаточно медленного изменения частоты входного сигнала.

Таким образом, выбор методов исследования динамических систем невелик, а удобство использования существенно зависит от возможностей ПС моделирования. Для исследования САУ электроприводами используются различные ПС, например, АЛМИК [1], МИК [2] и пакет программ МОДС/ПАЛС [3]. Все перечисленные ПС предполагают описание исследуемой системы в виде структурной схемы из набора базовых элементов и обеспечивают как простейший вид анализа - расчет переходных процессов, так и ряд вышеперечисленных сложных видов анализа и синтеза.

ПС МИК является наиболее развитым из рассматриваемых, выполняя почти все виды анализа и синтеза, но осуществляет их в пакетном режиме как на ЕС ЭВМ, так и на IBM PC, что не обеспечивает достаточной гибкости и удобства работы.

ПС МОДС/ПАЛС осуществляет расчет переходных процессов и частотный анализ численно-аналитическим методом для линейных систем (ПАЛС), а также многовариантный анализ, параметрическую оптимизацию и частотный анализ методом имитационного моделирования во временной области (МОДС). ПС также ориентировано на пакетный режим работы без сохранения результатов исследования, что существенно затрудняет его использование при работе со сложными моделями.

ПС АЛМИК обеспечивает удобную диалоговую работу в режиме многовариантного анализа с сохраняемыми результатами на сетке варьируемых параметров. Параметрическая оптимизация может быть легко осуществлена на этой же сетке параметров. Частотный анализ может быть легко выполнен путем имитационного моделирования во временной области, для чего используются такие базовые элементы, как генератор гармонического сигнала и анализаторы экстремумов и фазы.

Способы представления результатов так же существенно зависят от возможностей ПС. Ни одно из перечисленных ПС, кроме АЛМИК, не способно представить семейство графиков переходных процессов при различных значениях параметров (см. пример исследования в [1], стр.28) или изолинии равных значений показателей в плоскости двух параметров (см. пример исследования в [4]). Кроме того, существенной является ориентация АЛМИК на диалоговый режим работы, обеспечение сохранения и дальнейшего использования результатов исследования.

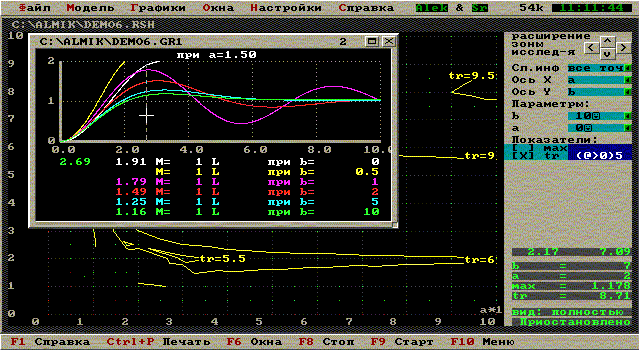
Диалоговая панель сложного исследования в АЛМИК

2. Организация диалоговой работы с исследованием в ПС АЛМИК.

При разработке подсистемы исследований в ПС АЛМИК была поставлена задача максимальной эргономичности работы с моделью, гибкости и полноты выбора способов представления результатов анализа. При этом использовались следующие положения:

2.1. Исследование проводится по следующим этапам:

• отладка модели путем расчета переходного процесса при определенных значениях параметров (определение структуры модели, ее постоянных параметров и настройка параметров численного интегрирования);
• подготовка модели к исследованию (указание изменяемых параметров и границ их изменения, задание режима исследования с указанием сохраняемых показателей и сигналов, служащих флагами ошибок и досрочного окончания моделирования, настройка графиков, которые можно будет получать по результатам исследования);
• автоматическое (в фоновом режиме) заполнение сетки параметров путем многократного моделирования;
• диалоговая работа с заполненной сеткой (расширение и углубление сетки как целиком, так и в выделенных диапазонах, оформление результатов в виде зависимостей или изолиний показателей в плоскости параметров, моделирование в указанных точках сетки и пр.);

2.2. Сетка параметров заполняется автоматически в фоновом режиме (в это время исследователь может, например, формировать графическое представление результатов, смотреть модель и графики переходных процессов).

2.3. В отличие от вышеперечисленных ПС, обеспечивается многосеансовый режим работы:

• файл с данными результатов исследования всегда сохраняется и становится неотъемлемой частью модели, автоматически загружается при загрузке модели; при этом модель защищается от изменений вплоть до закрытия (удаления) исследования;
• заполнение сетки автоматически продолжается при загрузке модели.

2.4. Унификация и удобство представления результатов:

• количество параметров и показателей может быть произвольно и определяется в тексте модели; результаты каждого очередного моделирования сохраняются в виде узлов сетки параметров с пометками успешного завершения, ошибки плавающей арифметики или логической ошибки моделирования (например, выхода показателя за допустимые пределы). Узлы, отмеченные как ошибочные, могут быть показаны на графике (например, для обозначения зоны неустойчивости), но не участвуют в дальнейшем построении графиков и изолиний;
• результаты представляются в виде плоской проекции, причем каждая ось координат может быть назначена на любой из параметров и показателей. При этом могут быть получены как графики зависимостей любого показателя от любого параметра, так и изолинии равных значений показателей в плоскости двух параметров (последняя задача решается путем разбиения сетки на треугольники и соответствующей интерполяции между ближайшими узлами сетки);
• при наличии ортогональных к плоскости изображения параметров можно построить семейства зависимостей (или изолиний) как при всех, так и при выделенных значениях этих параметров;
• изолинии равных значений показателей можно построить как с автоматическим выбором шага, так и при конкретных заданных значениях;
• наконец, предусмотрена автоматическая расстановка надписей на графиках и изолиниях с возможностью их дальнейшего редактирования.

2.5. Дополнительные функциональные возможности:

• ручное заполнение сетки исследования, применяемое для экономии времени при непрямоугольной форме интересующей исследователя области значений параметров либо для уточнения отдельных мест после заполнения основной сетки;
• моделирование в заданной точке сетки; при этом в случае выделения нескольких значений, ортогональных плоскости изображения параметров, будет произведено многократное моделирование при всех выделенных значениях параметров и построено семейство соответствующих графиков;
• контроль версий модели и данных исследования для исключения работы с устаревшими данными.

Диалоговое окно исследования, как и весь АЛМИК, выполнено в стандартном графическом интерфейсе Graphic Vision, разработанном автором. Все управляющие элементы интуитивно понятны и удобны для управления как с клавиатуры, так и с помощью манипулятора "мышь". С помощью мыши также производится указание точек и выделение зон на сетке, а также демонстрируются значения показателей в ближайших точках или под курсором на графике.

3. Реализация режима исследования.

При реализации режима исследования в соответствии с положениями п.2 был решен целый комплекс задач, краткое описание которых может представлять интерес для разработчиков исследовательских ПС и их пользователей.

3.1. Использование сетки параметров предполагает сохранение списка узлов и последующую работу с ними:

• автоматическое заполнение сетки производится с постоянным шагом (или по заданным в модели с помощью перечисляемого цикла значениям). Параметры очередного узла выбираются из условия отсутствия таких параметров в списке узлов, а также видимости данной точки и принадлежности ее выделенному диапазону (если таковой имеется); невидимые узлы будут рассматриваться только после заполнения видимой области;
• изображение в видимой плоскости строится на основе отсортированного списка узлов, в который не включаются узлы с пометкой ошибочного завершения. При успешном окончании моделирования с параметрами очередного узла он включается в отсортированный список и изображение в окне обновляется. Изменение параметров просмотра (назначение другого параметра на видимую ось координат и пр.) ведет к пересортировке списка узлов;
• в отсортированный список включаются и невидимые узлы, чтобы изменение выделенного для изображения набора графиков или изменение видимой зоны окна не приводили к длительной процедуре пересортировки.

3.2. Сортировка узлов для построения графика зависимости показателя от параметра выполняется таким образом, чтобы узлы с соседними значениями видимого параметра были рядом, тогда семейство графиков будет рисоваться путем простого линейного просмотра списка узлов.

3.3. Сортировка узлов для построения изолиний равных значений показателей представляет существенно более трудную задачу. Поскольку точное значение показателя для очередной изолинии очень редко может встретиться в каком-либо узле, для построения отрезка изолинии нужно вычислить координаты каждого его конца путем интерполяции между двумя ближайшими узлами сетки, значения показателей в которых охватывают требуемое значение. Для этого всю сетку надо разбить на возможно более компактные, не перекрывающие друг друга, элементарные геометрические фигуры - треугольники (процедура триангуляции).

Заметим, что геометрия сетки также влияет на эффективность анализа. Простой расчет показывает, что для плоскости наиболее выгодным является построение сетки по "сотовому" принципу, где разбиение происходит на равносторонние треугольники. При этом увеличение разрешающей способности сетки в 2 раза требует увеличения количества узлов в 3 раза, в то время как прямоугольная сетка - в 4 раза. Однако в АЛМИК используется прямоугольная сетка для удобства многомерных ее проекций (при числе параметров, большем 2).

Как было сказано выше, прямоугольная сетка заполняется автоматически. Однако простейший способ триангуляции такой сетки использовать нельзя, поскольку имеется возможность ручного указания новых узлов. Соответственно, была решена задача триангуляции произвольного набора узлов на плоскости:

• как только из списка неотсортированных узлов найдены три точки, которые могут образовать треугольник, они переносятся в список отсортированных, а в список треугольников вносится первый треугольник; кроме того, эти точки отмечаются как принадлежащие периметру;
• периметр должен обладать определенными свойствами - выпуклостью и определенной направленностью (в данном случае - по часовой стрелке);
• очередная точка из списка неотсортированных узлов может оказаться как снаружи, так и внутри периметра отсортированной области. Если точка находится снаружи периметра, следует построить все треугольники, включающие данную точку и две видимых точки периметра, чем достигается сохранение выпуклости периметра. Видимость определяется по знаку детерминанта тестируемого треугольника [6] (в данном случае видимым будет треугольник, обходимый против часовой стрелки). Если удалось построить хоть один треугольник, то данная точка включается в периметр (а точка в направленном внутрь углу треугольника из периметра исключается). Обнаружилось, что для устойчивой работы алгоритма при анализе детерминанта следует использовать некоторый запас, чтобы не рассматривать слишком "плоские" треугольники и не попасть при этом на "шероховатости" периметра, вызванные возможным разбросом одноименных координат узлов на линии сетки;
• если не удалось построить ни одного видимого треугольника, то точка лежит либо на самом периметре, либо внутри него. Тогда находятся все треугольники из списка, в которые попадает данная точка, и при возможности эти треугольники разбиваются данной точкой на два или три новых треугольника;
• наконец, для достижения наибольшего разрешения сетки производится компактизация треугольников, для чего просматриваются все пары из новых треугольников и сопряженных с ними сторонами. Если сопряженные треугольники образуют выпуклый четырехугольник, то он разбивается на два треугольника по наиболее короткой диагонали, после чего просмотр списка треугольников начинается заново.

3.4. Автоматическая расстановка надписей на графиках также является сложной задачей. Было предложено самое эффективное по скорости выполнения решение. Видимая область разбивается на знакоместа, и прорисовка каждого отрезка графика на экране сопровождается аналогичной прорисовкой отрезка в массиве знакомест, где помещается условный номер графика. Затем прямоугольник очередной надписи примеряется ко всем знакоместам и определяется положение, при котором он перекрывает минимальное количество знакомест с "чужим" графиком и совсем не перекрывает другие уже расставленные надписи. Если автоматически расставленные надписи не удовлетворяют исследователя, их можно передвинуть с помощью мыши или клавиатуры, отредактировать или вообще удалить. Интересно отметить, что такое поведение надписей в интерфейсе Graphic Vision обеспечено простой установкой флага "перемещаемости" у стандартного поля ввода строки и минимальными изменениями обработчика событий для реализации функции удаления.

3.5. Работа с такими показателями, как "время переходного процесса", выявило целый ряд проблем и потребовало создания соответствующих механизмов их решения. Первая проблема заключается в сложности достоверного определения времени переходного процесса. Обычно время переходного процесса определяют до момента вхождения сигнала в некоторую (например, 5%-ю) зону около установившегося значения. При заранее неизвестном максимальном времени переходного процесса целесообразно задать возможно большее максимальное время и сформулировать критерий досрочного окончания расчета. Для линейной системы небольшого порядка достаточно простого вхождения в зону при монотонном сигнале или обнаружения первого экстремума после вхождения в зону. Однако такой критерий будет недостаточен даже для линейной системы высокого порядка, тем более для нелинейных систем. В ПС АЛМИК используется эвристический критерий - время нахождения сигнала в заданной зоне в два раза больше промежутка времени от предыдущего выхода из зоны (или от начала расчета) до последнего момента вхождения в зону. При соблюдении этого критерия вторая переменная (флаг доверия) элемента TIMREG устанавливается равной первой переменной (времени переходного процесса) и может быть использована как более достоверный результат, а также как логический сигнал окончания цикла моделирования.

Вторая проблема состоит в обработке узлов с недостоверными занчениями показателей. В рассматриваемом случае, если время переходного процесса не будет с вышеописанной достоверностью зафиксировано по достижении максимально времени расчета, возможны два варианта возникновения узла с недостоверными значениями. Время переходного процесса будет либо неверно, если по достижении максимального времени расчета сигнал будет находиться в указанной зоне, либо будет равно нулю, если сигнал за пределами зоны. Это приведет как к искажению изолиний, так и к появлению паразитных, не соответствующих действительности изолиний вблизи этих узлов с нулевыми значениями.

Первого случая можно избежать, используя в качестве показателя второй (достоверный) сигнал элемента TIMREG, однако в ряде случаев заданного максимального времени расчета может не хватить для достоверного определеиня показателя, и в узле будет нулевое значение, что еще хуже. Во втором случае по результатам моделирования можно будет лишь сказать, что здесь время переходного процесса больше максимального времени.

Другим способом борьбы с недостоверными значениями в узле может быть признание результатов моделирования в данном узле ошибочными. Для этого следует в операторе RESEARCH предусмотреть ссылку на сигнал ошибки, вычисляемый в модели как "время больше или равно максимальному" и "флаг доверия не установлен". Однако это решение все равно не позволит исследователю получить реальную картину, поскольку при этом, например, узлы с устойчивыми, но слабо затухающими гармоническими колебаниями будут причислены к зоне неустойчивости. В качестве альтернативы можно предложить ряд способов гибкого решения проблемы уже после окончания моделирования - на этапе обработки и представления результатов:

• условие видимости узла для каждого из рассматриваемых показателей задается логическим выражением от значений параметров и показателей в данном узле. Если выражение для какого-либо узла ложно, то этот узел не используется при построении изолиний по данному показателю. Однако при этом в областях, близких к границе зоны ошибок, при использовании этого условия появятся разрывы изолиний;
• механизм изменения значений показателей позволит избежать вышеописанной ситуации путем временной (на период просмотра результатов) замены значений показателей в ряде узлов сетки. Например, можно заменить все нулевые значения показателя "время переходного процесса" на максимальное время моделирования. Однако при этом вместо вышеописанных разрывов изолиний вновь появятся паразитные изолинии (или локальные искажения вблизи таких спорных узлов. По-видимому, такой вариант наиболее предпочтителен, поскольку искажения изолиний невелики и носят только количественный, но не качественный характер (фактически изолинии будут только смещены в пределах шага между узлами, в то время как вблизи узлов с нулевыми значениями из-за интерполяции появлялись паразитные изолинии со значениями, стремящимися к нулю, что качественно неверно).

Таким образом, исследователь должен прийти к некоторому компромиссу при выборе между взаимно противоречивыми целями и параметрами исследования (шаг сетки, способ определения достоверности моделирования, максимально разрешенное время расчета) и выбрать приемлемые условия просмотра изолиний.

3.6. Из-за стремления к уменьшению времени расчета часто возникает соблазн увеличивать шаг интегрирования. Однако необходимо учитывать, что метод имитационного моделирования чувствителен к шагу интегрирования, при завышенных значениях будет увеличена колебательность переходных процессов или вообще получены неустойчивые решения. Шаг интегрирования следует выбирать по крайней мере в два раза меньше наименьшей постоянной времени модели.

3.7. При работе в режиме исследования исследователь может захотеть поменять в модели шаг интегрирования или другие параметры вроде максимального времени расчета. В таком случае АЛМИК предупредит о несоответствии версий модели и данных исследования, но при положительном ответе разрешит дальнейшую работу. Допускать этого, однако, не следует во избежание возможной разницы в данных старых и новых узлов сетки, что испортит построение изолиний и графиков. При необходимости придется повторить все исследование.

Единственным оправданным поводом для изменения модели при проведенном исследовании служит необходимость изменения списка вывода графиков (оператор OUTPUT) и операторов описания графиков.

3.8. Замечено, что исполняющая система АЛМИК по-разному обрабатывает ошибки плавающей арифметики на разных типах процессоров и операционных системах. Приемлемого решения здесь не видно, поэтому во избежание двусмысленных результатов исследователь должен сам грамотно составлять модель и исследование, не допуская работы при значениях параметров, явно делающих модель неустойчивой и могущих привести к ошибкам плавающей арифметики.

3.9. В вышеописанных процессах сортировки следует учитывать большое количество особых и вырожденных случаев (расположение точек в линию, "плоские" треугольники, точки на сторонах и вершинах треугольников, разброс координат узлов на одной линии сетки, невыпуклость двух сопряженных треугольников). При построении изолиний во всех вершинах треугольника может оказаться одинаковое значение показателя (в таком случае АЛМИК закрашивает весь треугольник). При длительном исследовании по окончании моделирования очередного узла обычно производится перерисовка окна, при этом следует обеспечивать, чтобы время перерисовки было не более 10% времени исследования. При реализации обработки команд пользователя следует учитывать все возможные состояния ПС (идет ли моделирование, есть ли выделенная область, нужно ли обновление окна или пересортировка узлов при данном изменении и т.д.). Наконец, случаются также ошибки в средствах разработки (в данном случае была найдена ошибка Borland Pascal при обработке сложных выражений и ряд ошибок графической библиотеки). Учет всех перечисленных особенностей представляет собой трудную задачу для разработчика, но необходим для создания полнофункционального, удобного и безошибочного программного продукта.

4. Пример сложного исследования.

Составим модель для исследования, изложенного в [4]. Представим передаточную функцию линейной динамической системы типа 2-1-2 в виде W(p)=(bp+1)/((b/a)p^3+bp^2+bp+1) и исследуем поведение системы в диапазоне параметров b=[0..10] и a=[0..10]. В данном случае заранее известно, что при значениях a и b, меньших 1, система неустойчива, однако данный пример носит демонстрационный характер и может показать много интересных особенностей.

Для задания параметров исследования в модели используются циклы. Заметим, что при a=0 в передаточной функции возникнет ошибка (деление на ноль). В процессе моделирования это не страшно, поскольку обработчик ошибок корректно прервет моделирование и пометит его результат как ошибочный. Однако в данном случае ошибка произойдет еще в процессе первоначальной трансляции модели, так как при обычной записи возрастающего цикла значение параметра полагается равным начальному. Во избежание такой ошибки цикл для параметра a следует записать как убывающий "a for (10,0,-1);".

Для анализа максимального значения сигнала используем элемент MAXIN, а для анализа времени переходного процесса - TIMREG, указывая 5% зону около установившегося значения, равного 1.

Для определения зоны неустойчивого (расходящегося) процесса будем иметь в виду, что в данном случае на границе устойчивости будут иметь место гармонические колебания с амплитудой 1 и постоянной составляющей 1. При этом для определения неустойчивости достаточно использовать критерий "сигнал больше 2", моделируемый элементом типа RELAY (для компенсации погрешности метода интегрирования следует взять значение, немного болшее 2). Сигнал этого элемента используем в двух местах - в описании основного цикла моделирования (для немедленного прекращения моделирования) и в операторе RESEARCH (для отметки типа "непригодный результат" в рассматриваемом узле сетки).

Кроме того, моделирование целесообразно завершить при достоверном определении показателя "время переходного процесса", для чего в описании основного цикла используется наряду с вышеупомянутым сигналом ошибки сигнал элемента TIMREG (вторая переменная состояния элемента, описываемая как "имя сигнала":1).

Максимальное время моделирования достаточно принять 10, а шаг интегрирования 0.01 обеспечивает приемлемую точность исследования, как установлено опытным путем.

Наконец, для возможности просмотра графиков переходных процессов внутри основного цикла моделирования следует задать оператор OUTPUT. Тогда при просмотре изолиний на плоскости параметров можно будет указать мышью любую точку и получить график переходного процесса с указанными параметрами. Если сделать то же самое при просмотре зависимостей, например, max=f(a), то будет получено семейство графиков переходных процессов при всех выбранных значениях параметра b.

{
	Демонстрация сложного исследования (директива RESEARCH)
	Исследуется система типа 2-1-2 W(p)=(bp+1)/((b/a)p3+bp2+bp+1)
}
v=1; step=0.01; tmax=10;
b	for	(0,10,1);
a	for	(10,0,-1);	{такое описание используется, чтобы не было 
				 ошибки b/a при первой трансляции}
t	for	(0,tmax,step)	(error + tr:1);
	{расчет оканчивается досрочно по сигналу ошибки или при достоверном
	 определении времени переходного процесса}
	L	L ((b)p+1/(b/a)p3+(b)p2+(b)p+1) (v); {исследуемая система}
	max	MaxIn  (0,tmax)    (L); {показатель "максимум"}
	tr	TimReg (0.95,1.05) (L); {показатель "время перех.процесса}
	error	Relay  (0,2.001,1) (L); {ошибкой считаем расходящийся процесс}
	output L;	stepout step;	{сигнал на график}
next;
research max,tr - error; {исследование с параметрами a,b (внешние циклы),
                          показателями max,tr и флагом ошибки error}
next; next;

После заполнения сетки с шагом 1 (что при заданных параметрах модели занимает 4 минуты машинного времени на iPentium-133 под Windows-95) будут в первом приближении получены контуры искомых номограмм, которые затем можно уточнить уменьшением шага сетки параметров. Уже в процессе расчета можно включать и выключать вывод отдельных изолиний, менять оси координат для построения различных зависимостей, задавать вывод графиков при определенных значениях параметров и осуществлять все необходимые манипуляции для наилучшего представления результатов.

Проиллюстрируем пути решения проблем, описанных в п. 3.5. Зададим вывод изолиний показателя tr (время переходного процесса), выделим интересующий нас диапазон сетки и расставим надписи (рис.1). Заметим, что около узла с неопределенным (нулевым) значением показателя (отмечен крестиком) искажаются изолинии, а также появляются паразитные изолинии со значениями от 5 до 0.

Рис.1. Паразитные изолинии около узлов с неверными значениями показателя

Для устранения искажений попробуем задать условие видимости узлов при построении изолиний показателя tr: (tr>0). В результате (рис.2) в окрестностях узлов с нулевыми значениями показателей появляются разрывы изолиний. Признаем такой способ представления результатов не очень удачным.

Рис.2. Исключение узлов с неверными значениями показателя

Следующая попытка заключается в замене нулевых значений показателя в узлах на большие значения, чтобы избежать появления паразитных изолиний. Для этого в разделе "замена показателей" укажем условие замены: tr=0 и новое, достаточно большое значение для таких узлов: 20.

Рис.3. Неудачная замена неверных значений показателя

Полученный результат (рис.3) говорит о том, паразитных изолиний уже нет, но проходящие в окрестности линии искажены из-за слишком большой разницы показателей между соседними узлами. Наилучшим будет задание значения, близкое к максимальному времени моделирования: 10 (рис.4).

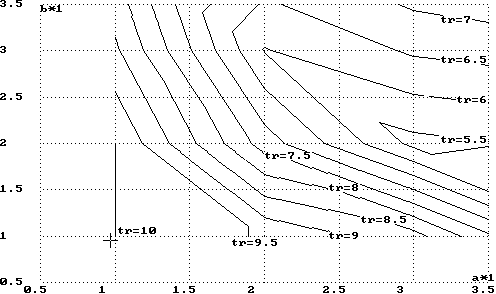
Рис.4. Удачная замена неверных значений показателя

Для дальнейшего уточнения необходимо уменьшить шаг сетки. Достаточно сделать это в ограниченном, наиболее интересном диапазоне (рис.5).

Рис.5. Искажения изолиний из-за неверных значений показателя, отличных от нуля

Теперь ясно видны локальные петлеобразные искажения изолиний, вызванные уже другой причиной - случайным попаданием сигнала в указанный диапазон в момент окончания моделирования (что хорошо видно по графику переходного процесса в одной из зон искажения). В этом случае значения показателя отличны от нуля, хотя и неверны, поэтому вышеописанные методы представления результата уже не помогают. Следовательно, исследование по данной модели недостоверно. Необходимы следующие изменения в модели:

• использование второй переменной элемента TIMREG, показывающей время переходного процесса более достоверно;
• увеличение максимального времени моделирования для уменьшения количества узлов с нулевыми значениями показателя.

Окончательный результат исследования представлен на рис.6.

Рис.6. Уточненное исследование

Список литературы:

1. Система имитационного моделирования АЛМИК: Методические указания по моделированию САУ/ Сост. А.Н.Донской, С.А.Лазарев. - Чебоксары, изд-во ЧГУ, 1991. 36 с.
2. Автоматизированный программный комплекс имитационного моделирования и поискового конструирования динамических систем. Руководство по эксплуатации.
3. Комплекс программ для автоматизации проектирования систем управления манипуляционных роботов: Учеб. пособие / под ред. Н.А.Лакоты / Моск.высш.техн.уч-ще. М.,1986, 36 с.
4. Н.В.Донской, А.Н.Донской. Упрощенный метод оценки качества переходных процессов в замкнутой САУ с ЛАЧХ разомкнутого контура типа 2-1-2: Технические науки: сегодня и завтра: Тез. докл. юбилейной итоговой научной конференции. Чебоксары: Изд-во Чуваш.ун-та, 1997. С. 101-102.
5. Поздеев А.Д., Аристархов О.Г., Волков Д.Н. Чувствительность асинхронных регулируемых электроприводов с частотно-токовым управлением к неточности задания параметров настройки// Электротехника. 1998. № 6. С. 1-7.
6. Л.Аммерал. Принципы программирования в машинной графике. Пер. С англ. - М.: "Сол Систем", 1992. - 205 с.

См. также: "Развитие системы имитационного моделирования АЛМИК"

Home Page http://simulators.narod.ru

Post: 428000, г.Чебоксары, а/я 121, Донской Алексей Николаевич

Download Almik DPMI Download Almik real mode Установка и настройки